Biblio
Filters: Author is Balandat, Maximilian [Clear All Filters]
.
2015. The Hedge Algorithm on a Continuum. Proceedings of the 32nd International Conference on Machine Learning (ICML-15). :824-832.
ABSTRACT: We consider an onlinse optimization problem on a compact subset S ⊂ Rn (not necessarily convex), in which a decision maker chooses, at each iteration t, a probability distribution xover S, and seeks to minimize a cumulative expected loss, 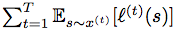 , where ℓ(t) is a Lipschitz loss function revealed at the end of iteration t. Building on previous work, we propose a generalized Hedge algorithm and show a
, where ℓ(t) is a Lipschitz loss function revealed at the end of iteration t. Building on previous work, we propose a generalized Hedge algorithm and show a 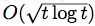 bound on the regret when the losses are uniformly Lipschitz and S is uniformly fat (a weaker condition than convexity). Finally, we propose a generalization to the dual averaging method on the set of Lebesgue-continuous distributions over S.
bound on the regret when the losses are uniformly Lipschitz and S is uniformly fat (a weaker condition than convexity). Finally, we propose a generalization to the dual averaging method on the set of Lebesgue-continuous distributions over S.



