 CNLN Problem Instance: Neuron
CNLN Problem Instance: Neuron
This is the FitzHugh-Nagumo Neuron Model, proposed in the ARCH paper "Benchmarks for Non-linear Continuous System Safety Verification", by Andrew Sogokon, Taylor T Johnson and Khalil Ghorbal.
It is a 2-d system with the following nonlinear dynamics:
x' = x - x^3 / 3 - y + 7/8
y' = 0.08 * (x + 0.7 - 0.8*y)
As in the benchmark paper the initial states are taken to be x = [-1, -0.5] and y = [1.0, 1.5]. A time bound of 40 is sufficient to complete a limit cycle. Two instances are proposed with a modified safety condition where, if the unsafe states are y >= 1.8, the system should be safe, and if y >= 1.6 is used for the unsafe states, then the system is unsafe. I've attached SpaceEx .cfg and .xml files for this benchmark. Although you can't run them in SpaceEx (since there are nonlinear dynamics), they can be converted to other tools which do support nonlinear dynamics using Hyst.
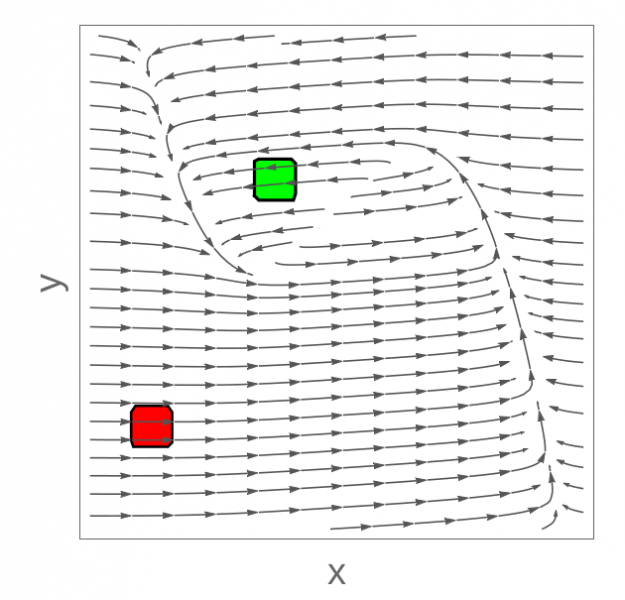
Here's a plot from the benchmark paper. We use the same initial (green states), but a modified set of unsafe states (not the red ones shown in the plot).
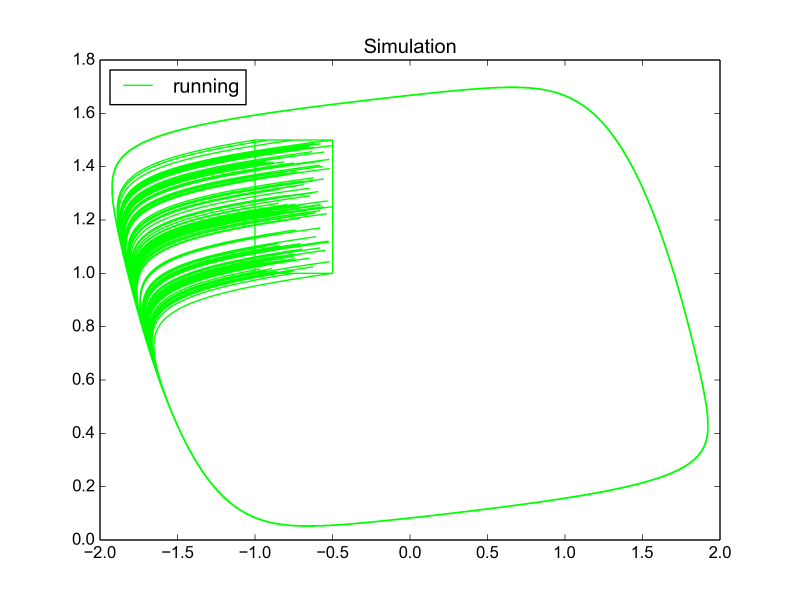
Here's a simulation from the corners of the initial states and 100 random points:
This system is 2-d and was analyzed in a few papers, so hopefully it's compatible with many tools.
Original paper: R. FitzHugh. "Impulses and physiological states in theoretical models of nerve membrane." Biophysical J, 1961.
Other papers which use this model:
T. Dang and R. Testylier, "Reachability analysis for polynomial dynamical systems using the Bernstein expansion.", Reliable Computing Journal, 2012.
M.A. Ben Sassi, A. Girard, and S. Sankaranarayanan. "Iterative computation of polyhedral invariants sets for polynomial dynamical systems.", CDC, 2014.
| Attachment | Size |
|---|---|
| bytes | |
| bytes |

