CAFF Problem Instance: Space Station
The system is a continuous linear time-invariant system x' = Ax + Bu proposed as a benchmark in ARCH 2016 [1]: "International Space Station (ISS). The ISS state-space model presented in this paper is a structural model of component 1R (Russian service module) of the International Space Station. It has 270 state variables with three inputs."
The specification deals with the possible range for output y_3, which is a linear combination of the state variables (y = Cx). Initially all 270 variables are in the range [-0.0001, 0.0001], u_1 is in [0, 0.1], u_2 is in [0.8, 1], and u_3 is in [0.9, 1]. The time bound is 20, with a suggested step size of 0.005. A Matlab-compatible .mat file (that can also be opened with Python using scipy.io.loadmat) that defines the A, B, and C matrices is available here: http://slicot.org/objects/software/shared/bench-data/iss.zip . Both a safe and unsafe specification is available for the case where the inputs are constant [2], and when the inputs are time-varying [3], so this problem has four instances.
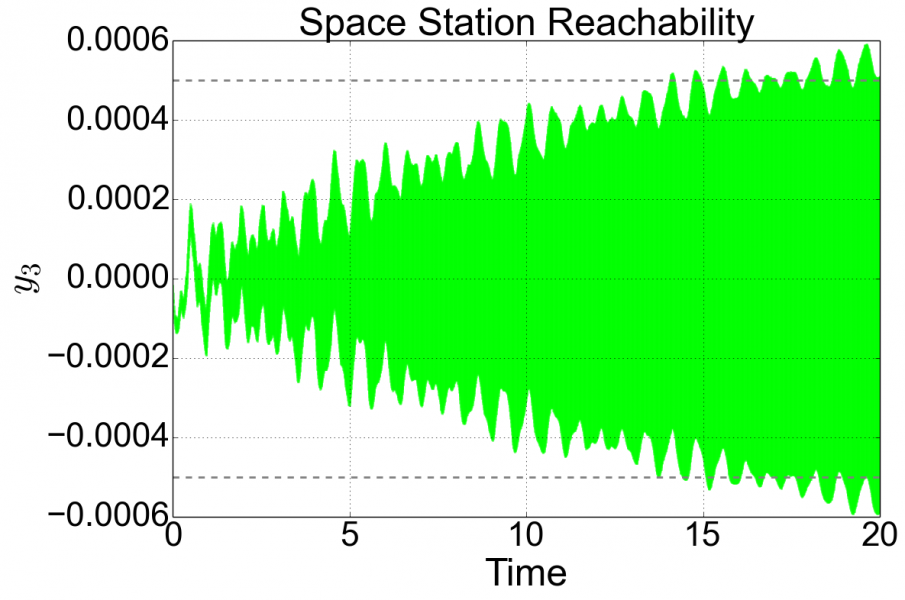
In the constant-input case, the specification y_3 \in [-0.00017, 0.00017] is violated around time ~0.5, whereas the specification y_3 \in [-0.0005, 0.0005] is safe. For the time-varying case, the specification y_3 \in [-0.0005, 0.0005] is violated around time ~13.7, whereas the specification y_3 \in [-0.0007, 0.0007] is safe.
Plots of the fixed input case is below, including a zoomed-in version showing the violation starting at time 0.0498:
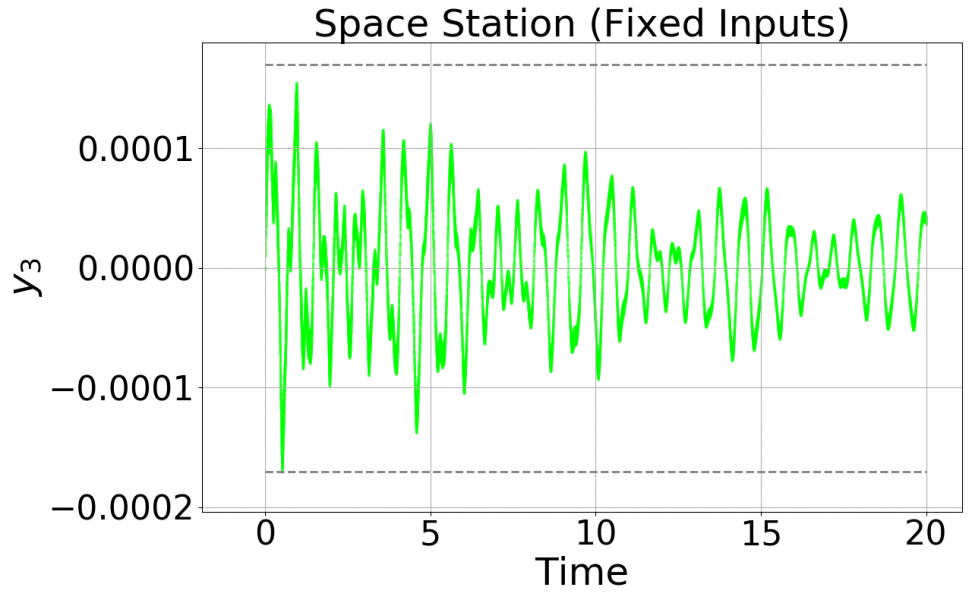
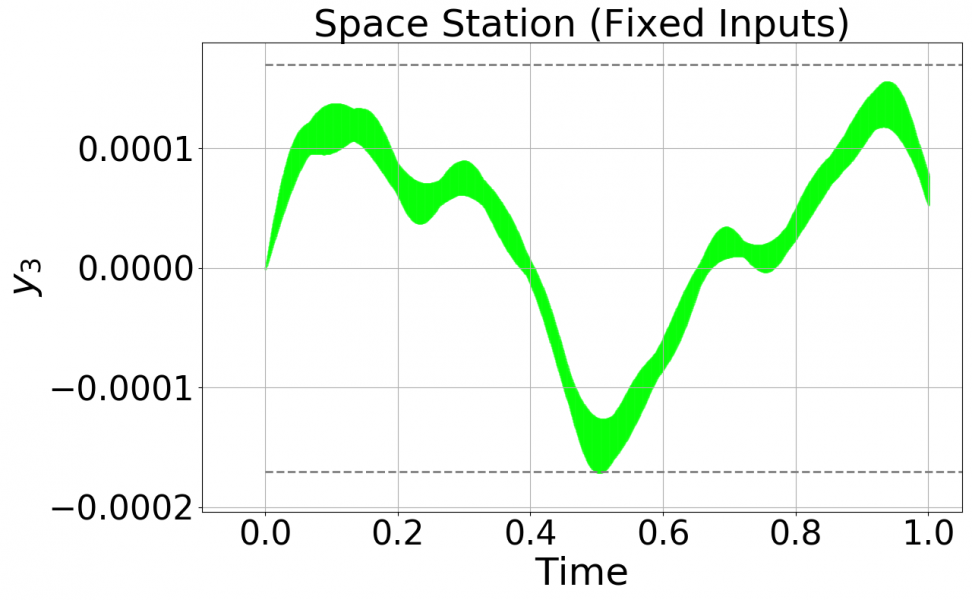
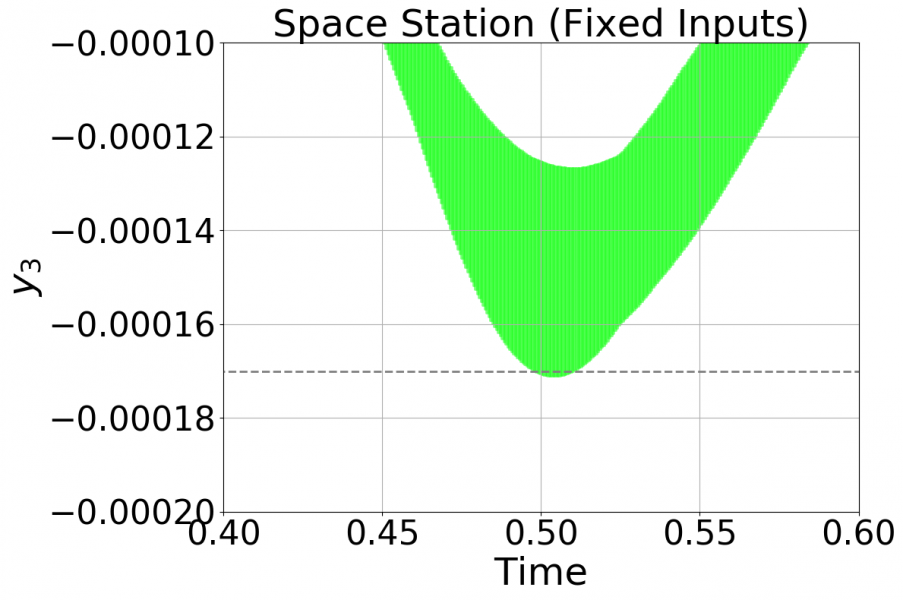
A plot of the time-varying inputs case is below:
[1] H. D. Tran, L. V. Nguyen, and T. T. Johnson. "Large-scale linear systems from order-reduction" 3rd Applied Verification for Continuous and Hybrid Systems Workshop (ARCH 2016)
[2] "Direct Verification of Linear Systems with over 10000 Dimensions", S. Bak, P. Duggirala, 4th International Workshop on Applied Verification for Continuous and Hybrid Systems (ARCH 2017)
[3] "Simulation-Equivalent Reachability of Large Linear Systems with Inputs", S. Bak, P. Duggirala, 29th International Conference on Computer-Aided Verification (CAV 2017)
Looks interesting. Should we also provide a version with uncetain inputs?
In all the ISS models, the variables y1, y2, and y3 are declared as controlled. However, I think that they should all be uncontrolled.
The results obtained with the decomposition algorithm implemented in JuliaReach are shown in this notebook. Both dense time and discrete time are shown, for time-varying and for constant inputs. Comments welcome.
We found that for the time-varying input case, the specification "y3 [0.0007,0.0007] is safe" is not satisfied. As outlined previously in [1], we think that the main reason is that the property involves a linear combination of several (half the total) of state variables from different blocks. Hence, low-dim set types such as interval decomposition (1D) or epsilon-close polygons (2D) are not accurate for this property.
On the other hand, for the constant input case, both specifications are validated.
We found that delaying the overapproximation of the sets W(k) due to the inputs (cf. Eq. (19) in the HSCC paper), the specification 2, y3[0.0007,0.0007], is satisfied.
The insight comes from the fact that overapproximating the sequence W(k) at each time step produces a small error that may accumulate, while overapproximating only over multiples of k, and keeping it lazy the rest of the time, is usually slower (it depends) but more accurate.
A further optimization can be used: for querying a fixed direction of W(k+1), (property checking mode), the Minkowski sum array can cache the previously computed support vector for the k-size array, only having to evaluate at each time the newly added set and take 1 vector sum.
Neat.
Does the :lazy_inputs_interval=>40000, method show the violation of y3SPEC1? At what time step does this occur?
Also, the time-varying plot looks much wider, can this be produced with :lazy_inputs_interval=>40000 as well?
> Does the :lazy_inputs_interval=>40000, method show the violation of y3SPEC1? At what time step does this occur?
Yes. For continuous time and step size `6e-4`, i get:
`[info] The property may be violated at index 16060, (time point 9.636)!`
While for discrete time and step size `5e-3`, i get:
`[info] The property may be violated at index 2743, (time point 13.715)!`
> Also, the time-varying plot looks much wider, can this be produced with :lazy_inputs_interval=>40000 as well?
You hit an interesting point that deserves further discussion. The short answer is "no", at the moment we do not get reachability plots with better accuracy with the new lazy inputs option :(
There is a crucial difference, by design, between the "check" mode and the "reach" mode (this is the mode needed for plotting). In the former, since we don't really need to evaluate support functions of the individual blocks, but only the support vector of the given linear combination (the given property), we keep the blocks `Xhatk[i]` lazy, as in line [1].
On the other hand, for the "reach" mode we want to return all the concrete sequence of sets, thus `Xhatk[i]` are concretized, or overapproximated, at each time step, as in line [2].
In sum, it seems that there is room for improvement on the accuracy of the time-varying plots, if we mix the approaches in "reach" and "check"..
Thanks for the feedback. BTW, i've updated the notebook with these results.
[1] https://github.com/JuliaReach/Reachability.jl/blob/master/src/Properties/check_blocks.jl#L85
[2] https://github.com/JuliaReach/Reachability.jl/blob/master/src/ReachSets/reach_blocks.jl#L83
Hi Matthias,
On the CORA plot for the uncertain case, it looks like the safe spec, ISS01, is violated. Is the plot using different parameters from the verification?
Dear all,
as all structural vibration problems, the international space station is not an exception in having very high resonance frequencies. Since some tools assume constant inputs between time steps, they do not hit those resonance frequencies. Cora, however, captures all frequencies.
@Stan: Could you decrease the step size dramatically and tell us what the effect is with your tool?
This aspect has to be clearly addressed in the report.
Best,
Matthias
While what you said about handling all frequencies is true, I don't think the effect is that dramatic on this problem. With JuliaReach "specification 2, y3[0.0007,0.0007], is satisfied". JuliaReach, as far as I know, doesn't assume constant inputs between steps, so I don't think that's the issue.
I wrote a script that uses Hylaa to find the maximum spec (y3 \in [-limit, limit]) that is still safe for various time steps, using a binary search strategy up to some tolerance (1e-6). This is the result:
Steps=200; Step_size=0.1, Max_Safe = 0.000528125
Steps=400; Step_size=0.05, Max_Safe = 0.000578125
Steps=800; Step_size=0.025, Max_Safe = 0.00059375
Steps=1600; Step_size=0.0125, Max_Safe = 0.00059765625
Steps=3200; Step_size=0.00625, Max_Safe = 0.00059921875
Steps=6400; Step_size=0.003125, Max_Safe = 0.00059921875
Steps=12800; Step_size=0.0015625, Max_Safe = 0.00059921875
Steps=25600; Step_size=0.00078125, Max_Safe = 0.00059921875
Steps=51200; Step_size=0.000390625, Max_Safe = 0.00059921875
Steps=102400; Step_size=0.0001953125, Max_Safe = 0.00059921875
Based on this, even with a small time step, the maximum safe value is far from the spec value of 0.0007 (and is very far from the 0.0015 that looks reachable in the CORA plot), so I think the spec should be safe.
Matthias, could you reduce the step size on CORA and see how much that changes the maximum value in the spec that is satisfied?
Dear Stan,
first of all: I'm sorry for making a statement before checking it. I should have first checked the Bode plot first, which shows that there is no large resonance at a high frequency:
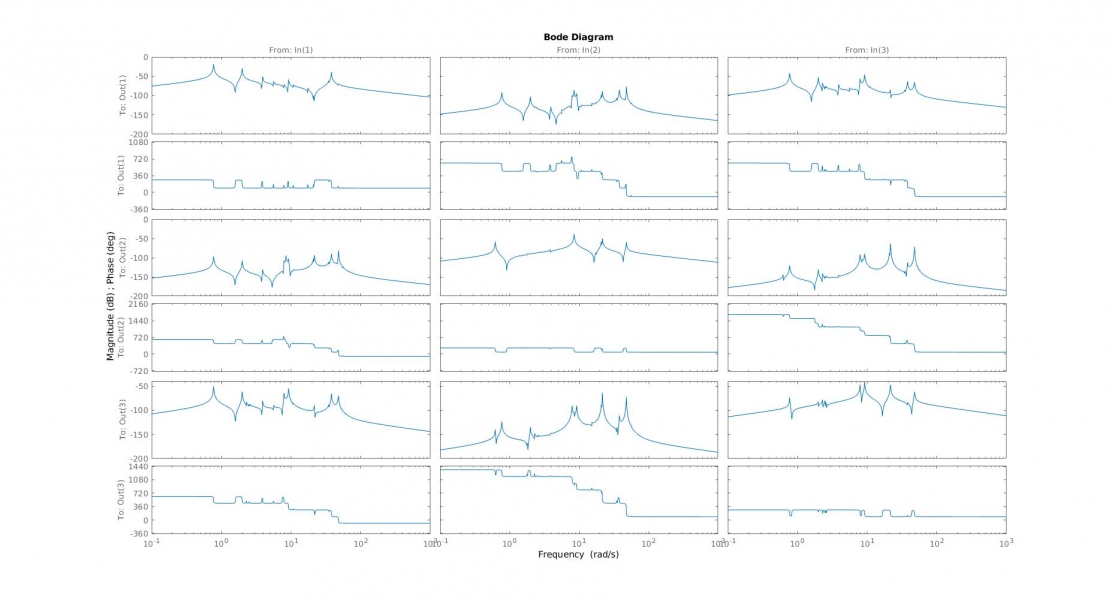
My PhD student Niklas did not know that there is a more or less hidden setting that was chosen wrong. I have corrected it and the results are much tighter:
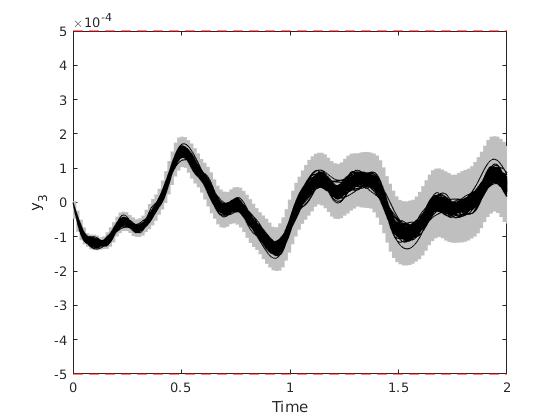
I hope I could clarify this issue. Niklas is on vacation next week, but he'll update the results in Overleaf afterwards. I am also busy traveling next week.
Best,
Matthias
That plot looks better. For reference, here's what I get for the first two seconds. It looks similar to yours, but I think one of us has a sign error for y_3. The JuliaReach one has the reach set initially going up as well.
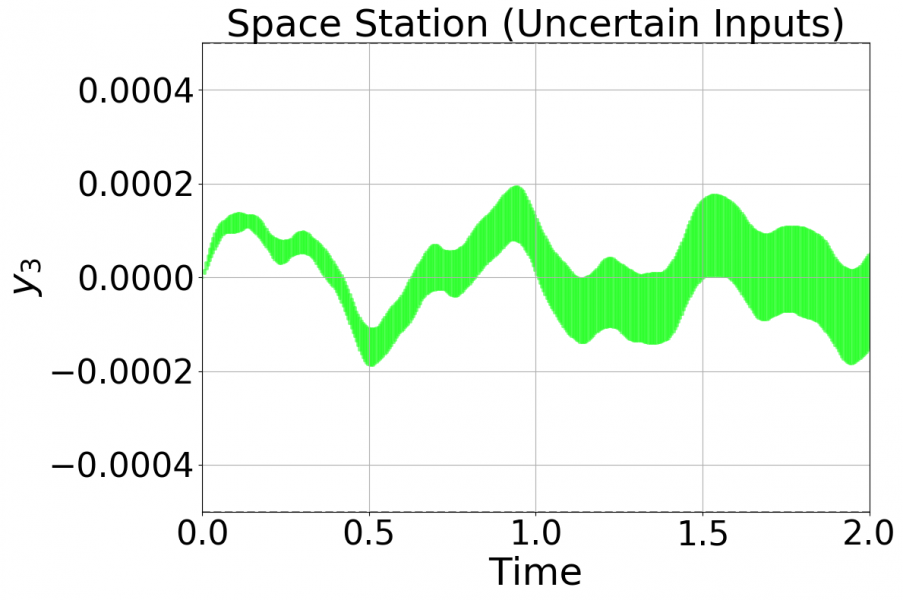
When I said the time-varying inputs case I think I meant the uncertain inputs case, so that's covered (the last plot is this system which has a different spec).