Biblio
Assuring communication integrity is a central problem in security. However, overhead costs associated with cryptographic primitives used towards this end introduce significant practical implementation challenges for resource-bounded systems, such as cyber-physical systems. For example, many control systems are built on legacy components which are computationally limited but have strict timing constraints. If integrity protection is a binary decision, it may simply be infeasible to introduce into such systems; without it, however, an adversary can forge malicious messages, which can cause signi cant physical or financial harm. We propose a formal game-theoretic framework for optimal stochastic message authentication, providing provable integrity guarantees for resource-bounded systems based on an existing MAC scheme. We use our framework to investigate attacker deterrence, as well as optimal design of stochastic message authentication schemes when deterrence is impossible. Finally, we provide experimental results on the computational performance of our framework in practice.
Cheap ubiquitous computing enables the collectionof massive amounts of personal data in a wide variety of domains.Many organizations aim to share such data while obscuring fea-tures that could disclose identities or other sensitive information.Much of the data now collected exhibits weak structure (e.g.,natural language text) and machine learning approaches havebeen developed to identify and remove sensitive entities in suchdata. Learning-based approaches are never perfect and relyingupon them to sanitize data can leak sensitive information as aconsequence. However, a small amount of risk is permissiblein practice, and, thus, our goal is to balance the value ofdata published and the risk of an adversary discovering leakedsensitive information. We model data sanitization as a gamebetween 1) a publisher who chooses a set of classifiers to applyto data and publishes only instances predicted to be non-sensitiveand 2) an attacker who combines machine learning and manualinspection to uncover leaked sensitive entities (e.g., personal names). We introduce an iterative greedy algorithm for thepublisher that provably executes no more than a linear numberof iterations, and ensures a low utility for a resource-limitedadversary. Moreover, using several real world natural languagecorpora, we illustrate that our greedy algorithm leaves virtuallyno automatically identifiable sensitive instances for a state-of-the-art learning algorithm, while sharing over 93% of the original data, and completes after at most 5 iterations.
Starting with the seminal work by Kempe et al., a broad variety of problems, such as targeted marketing and the spread of viruses and malware, have been modeled as selecting
a subset of nodes to maximize diffusion through a network. In
cyber-security applications, however, a key consideration largely ignored in this literature is stealth. In particular, an attacker often has a specific target in mind, but succeeds only if the target is reached (e.g., by malware) before the malicious payload is detected and corresponding countermeasures deployed. The dual side of this problem is deployment of a limited number of monitoring units, such as cyber-forensics specialists, so as to limit the likelihood of such targeted and stealthy diffusion processes reaching their intended targets. We investigate the problem of optimal monitoring of targeted stealthy diffusion processes, and show that a number of natural variants of this problem are NP-hard to approximate. On the positive side, we show that if stealthy diffusion starts from randomly selected nodes, the defender’s objective is submodular, and a fast greedy algorithm has provable approximation guarantees. In addition, we present approximation algorithms for the setting in which an attacker optimally responds to the placement of monitoring nodes by adaptively selecting the starting nodes for the diffusion process. Our experimental results show that the proposed algorithms are highly effective and scalable.
The quantity of personal data gathered by service providers via our daily activities continues to grow at a rapid pace. The sharing, and the subsequent analysis of, such data can support a wide range of activities, but concerns around privacy often prompt an organization to transform the data to meet certain protection models (e.g., k-anonymity or E-differential privacy). These models, however, are based on simplistic adversarial frameworks, which can lead to both under- and over-protection. For instance, such models often assume that an adversary attacks a protected record exactly once. We introduce a principled approach to explicitly model the attack process as a series of steps. Specically, we engineer a factored Markov decision process (FMDP) to optimally plan an attack from the adversary's perspective and assess the privacy risk accordingly. The FMDP captures the uncertainty in the adversary's belief (e.g., the number of identied individuals that match the de-identified data) and enables the analysis of various real world deterrence mechanisms beyond a traditional protection model, such as a penalty for committing an attack. We present an algorithm to solve the FMDP and illustrate its efficiency by simulating an attack on publicly accessible U.S. census records against a real identied resource of over 500,000 individuals in a voter registry. Our results demonstrate that while traditional privacy models commonly expect an adversary to attack exactly once per record, an optimal attack in our model may involve exploiting none, one, or more indiviuals in the pool of candidates, depending on context.
Stackelberg game models of security have received much attention, with a number of approaches for
computing Stackelberg equilibria in games with a single defender protecting a collection of targets. In contrast, multi-defender security games have received significantly less attention, particularly when each defender protects more than a single target. We fill this gap by considering a multi-defender security game, with a focus on theoretical characterizations of equilibria and the price of anarchy. We present the analysis of three models of increasing generality, two in which each defender protects multiple targets. In all models, we find that the defenders often have the incentive to over protect the targets, at times significantly. Additionally, in the simpler models, we find that the price of anarchy is unbounded, linearly increasing both in the number of defenders and the number of targets per defender. Surprisingly, when we consider a more general model, this results obtains only in a “corner” case in the space of parameters; in most cases, however, the price of anarchy converges to a constant when the number of defenders increases.
ABSTRACT: We consider an onlinse optimization problem on a compact subset S ⊂ Rn (not necessarily convex), in which a decision maker chooses, at each iteration t, a probability distribution xover S, and seeks to minimize a cumulative expected loss,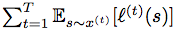 
, where ℓ(t) is a Lipschitz loss function revealed at the end of iteration t. Building on previous work, we propose a generalized Hedge algorithm and show a 
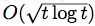bound on the regret when the losses are uniformly Lipschitz and S is uniformly fat (a weaker condition than convexity). Finally, we propose a generalization to the dual averaging method on the set of Lebesgue-continuous distributions over S.
We examine the problem of aggregating the results of multiple anti-virus (AV) vendors' detectors into a single authoritative ground-truth label for every binary. To do so, we adapt a well-known generative Bayesian model that postulates the existence of a hidden ground truth upon which the AV labels depend. We use training based on Expectation Maximization for this fully unsupervised technique. We evaluate our method using 279,327 distinct binaries from VirusTotal, each of which appeared for the rst time between January 2012 and June 2014.
Our evaluation shows that our statistical model is consistently more accurate at predicting the future-derived ground truth than all unweighted rules of the form \k out of n" AV detections. In addition, we evaluate the scenario where partial ground truth is available for model building. We train a logistic regression predictor on the partial label information. Our results show that as few as a 100 randomly selected training instances with ground truth are enough to achieve 80% true positive rate for 0.1% false positive rate. In comparison, the best unweighted threshold rule provides only 60% true positive rate at the same false positive rate.
As our ground transportation infrastructure modernizes, the large amount of data being measured, transmitted, and stored motivates an analysis of the privacy aspect of these emerging cyber-physical technologies. In this paper, we consider privacy in the routing game, where the origins and destinations of drivers are considered private. This is motivated by the fact that this spatiotemporal information can easily be used as the basis for inferences for a person's activities. More specifically, we consider the differential privacy of the mapping from the amount of flow for each origin-destination pair to the traffic flow measurements on each link of a traffic network. We use a stochastic online learning framework for the population dynamics, which is known to converge to the Nash equilibrium of the routing game. We analyze the sensitivity of this process and provide theoretical guarantees on the convergence rates as well as differential privacy values for these models. We confirm these with simulations on a small example.