The Hedge Algorithm on a Continuum

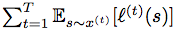ABSTRACT: We consider an onlinse optimization problem on a compact subset S Rⁿ (not necessarily convex), in which a decision maker chooses, at each iteration t, a probability distribution xover S, and seeks to minimize a cumulative expected loss, , where l^(t) is a Lipschitz loss function revealed at the end of iteration 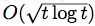t. Building on previous work, we propose a generalized Hedge algorithm and show a bound on the regret when the losses are uniformly Lipschitz and S is uniformly fat (a weaker condition than convexity). Finally, we propose a generalization to the dual averaging method on the set of Lebesgue-continuous distributions over S.