 Bifurcation Analysis of Cardiac Alternans using delta-Decidability Poster.pdf
Bifurcation Analysis of Cardiac Alternans using delta-Decidability Poster.pdf
We present a bifurcation analysis of electrical alternans in the two-current Mitchell-Schaeffer (MS) cardiac-cell model using the theory of 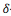 -decidability over the reals. Electrical alternans is a phenomenon characterized by a variation in the successive Action Potential Durations (APDs) generated by a single cardiac cell or tissue. Alternans are known to initiate re-entrant waves and are an important physiological indicator of an impending life-threatening arrhythmia such as ventricular fibrillation. The bifurcation analysis we perform determines, for each control parameter
-decidability over the reals. Electrical alternans is a phenomenon characterized by a variation in the successive Action Potential Durations (APDs) generated by a single cardiac cell or tissue. Alternans are known to initiate re-entrant waves and are an important physiological indicator of an impending life-threatening arrhythmia such as ventricular fibrillation. The bifurcation analysis we perform determines, for each control parameter 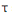 of the MS model, the bifurcation point in the range of
of the MS model, the bifurcation point in the range of 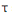 such that a small perturbation to this value results in a transition from alternans to non-alternans behavior. To the best of our knowledge, our analysis represents the first formal verification of non-trivial dynamics in a numerical cardiac-cell model.
such that a small perturbation to this value results in a transition from alternans to non-alternans behavior. To the best of our knowledge, our analysis represents the first formal verification of non-trivial dynamics in a numerical cardiac-cell model.
Our approach to this problem rests on encoding alternans-like behavior in the MS model as a 11-mode, multinomial hybrid automaton (HA). For each model parameter, we then apply a sophisticated, guided-search- based reachability analysis to this HA to estimate parameter ranges for both alternans and non-alternans behavior. The bifurcation point separates these two ranges, but with an uncertainty region due to the under- lying 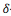 - decision procedure. This uncertainty region, however, can be re- duced by decreasing
- decision procedure. This uncertainty region, however, can be re- duced by decreasing 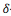 at the expense of increasing the model exploration time. Experimental results are provided that highlight the effectiveness of this method.
at the expense of increasing the model exploration time. Experimental results are provided that highlight the effectiveness of this method.
 PDF document
PDF document- 1.62 MB
- 18 downloads
- Download
- PDF version
- Printer-friendly version
